Differentiation of Trigonometric Functions | A Level Maths Revision Notes

Contents hide

1 Summary

1.1 Differentiation of sin(x) and cos(x)

1.2 Differentiation of tan(x)

1.3 Differentiation of sec(x)

1.4 Differentiation of cosec(x)

1.5 Example 1

Summary

Remember these derivatives of the trigonometric functions:

$\frac { d }{ dx } \sin { (x) } \quad =\quad \cos { (x) }$
$\frac { d }{ dx } \cos { (x) } \quad =\quad -\sin { (x) } \quad$
$\frac { d }{ dx } \tan { (x) } \quad =\quad { sec }^{ 2 }(x)$
$\frac { d }{ dx } \cot { (x) } \quad =\quad -co{ sec }^{ 2 }(x)$
$\frac { d }{ dx } \sec { (x) } \quad =\quad \sec { (x) } \tan { (x) }$
$\frac { d }{ dx } cosec(x)\quad =\quad -cosec(x)\cot { (x) }$

Differentiation of sin(x) and cos(x)

To begin with, we know that differentiation is a method to find the gradient of a curve.

Rule of differentiation is if $y\quad =\quad { x }^{ n }$ , then $\frac { dy }{ dx } \quad =\quad n{ x }^{ n\quad -\quad 1 }$ . However in this article we will focus entirely on differentiation of trigonometric functions.

Consider the graph of $y\quad =\quad \sin { (x) }$ in the range $0\quad \le \quad x\quad \le \quad 2\pi$ . We draw tangents to the sin curve at the points where $x\quad =\quad 0,\quad x\quad =\quad \frac { \pi }{ 2 } ,\quad x\quad =\quad \pi ,\quad x\quad =\quad \frac { 3\pi }{ 2 } ,\quad x\quad =\quad 2\pi$ radians.

x	0	$\frac { \pi }{ 2 }$	$\pi$	$\frac { 3\pi }{ 2 }$	$2\pi$
sin(x)	0	1	0	-1	0

We now plot the values of the gradients of these tangents and we obtain a graph of cos(x). As shown in Fig 2.

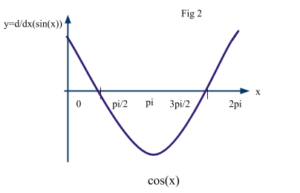
Hence, this shows that derivative of sin(x) is cos(x). It can be written as:

$\frac { d }{ dx } \sin { (x) } \quad =\quad \cos { (x) }$ when x in radians.

Similarly, we can find that:

$\frac { d }{ dx } \cos { (x) } \quad =\quad -\sin { (x) } \quad$

Differentiation of tan(x)

Let’s assume $y\quad =\quad \tan { (x) }$ ,

$y\quad =\quad \frac { \sin { (x) } }{ \cos { (x) } }$ using quotient rule

$\frac { dy }{ dx } \quad =\quad \frac { \cos { (x)\cos { (x) } \quad -\quad \sin { (x) } (-\sin { (x) } ) } }{ { (\cos { (x) } ) }^{ 2 } }$

$\frac { dy }{ dx } \quad =\quad \frac { { cos }^{ 2 }(x)\quad +\quad { sin }^{ 2 }(x) }{ { cos }^{ 2 }(x) }$

$\frac { dy }{ dx } \quad =\quad \frac { 1 }{ { cos }^{ 2 }(x) } \quad =\quad { sec }^{ 2 }(x)$

Differentiation of sec(x)

Let’s assume: $y\quad =\quad \sec { (x) }$ , $y\quad =\quad { cos }^{ -1 }(x)$

$\frac { dy }{ dx } \quad =\quad -1({ cos }^{ -2 }(x))(-\sin { (x) } )$

$\frac { dy }{ dx } \quad =\quad \frac { \sin { (x) } }{ { cos }^{ 2 }(x) } \quad =\quad (\frac { \sin { (x) } }{ \cos { (x) } } )(\frac { 1 }{ \cos { (x) } } )$

$\frac { d }{ dx } sec(x)\quad =\quad sec(x)tan(x)$

Differentiation of cosec(x)

Assume $y\quad =\quad cosec(x)\quad =\quad \frac { 1 }{ \sin { (x) } } \quad =\quad { sin }^{ -1 }(x)$

Taking the derivative:

$\frac { dy }{ dx } \quad =\quad -1({ sin }^{ -2 }(x))\cos { (x) }$

$\frac { dy }{ dx } \quad =\quad \frac { -cos(x) }{ { sin }^{ 2 }(x) }$

$\frac { dy }{ dx } \quad =\quad -(\frac { \cos { (x) } }{ \sin { (x) } } )(\frac { 1 }{ \sin { (x) } } )$

$\frac { dy }{ dx } \quad =\quad -cot(x)cosec(x)$

$\frac { d }{ dx } cosec(x)\quad =\quad -cot(x)cosec(x)$

Hence, to conclude derivatives of trigonometric functions are:

$\frac { d }{ dx } \sin { (x) } \quad =\quad \cos { (x) }$ $\frac { d }{ dx } \cos { (x) } \quad =\quad -\sin { (x) } \quad$ $\frac { d }{ dx } \tan { (x) } \quad =\quad { sec }^{ 2 }(x)$ $\frac { d }{ dx } \cot { (x) } \quad =\quad -co{ sec }^{ 2 }(x)$ $\frac { d }{ dx } \sec { (x) } \quad =\quad \sec { (x) } \tan { (x) }$ $\frac { d }{ dx } cosec(x)\quad =\quad -cosec(x)\cot { (x) }$