Integration Techniques | Summary & Examples

Contents hide

1 Summary

1.1 Rules of Integration

1.2 Integration of trigonometric functions

1.3 Example #1

1.4 Integration of exponential functions

1.5 Example #2

1.6 Integration of

1.7 Example #3

1.8 Integrating Fractions

1.9 Example #4

Summary

Integration techniques include:

Integration of trigonometric functions: $\frac { d }{ dx } f\left( x \right) \quad =\quad g\left( x \right) \quad \Rightarrow \quad \int { g\left( x \right)dx\quad =\quad f\left( x \right)\quad +\quad C }$
Integration of exponential functions: $\frac { d }{ dx } { (e }^{ x })\quad =\quad { e }^{ x }$
Integration of $\frac { 1 }{ x }$ : $\int { \frac { f^{ ' }\left( x \right) }{ f\left( x \right) } } dx\quad =\quad \ln { \left| f\left( x \right) \right| } \quad +\quad C$
Integrating Fractions: This involves $\frac { 1 }{ x }$ , numerator is the derivative of a function within the denominator and lastly partial fractions.

We know that the process of antidifferentiation is called integration.

Clearly if $\quad \frac { dy }{ dx } \quad =\quad { x }^{ n }$ then $\quad y\quad =\quad \frac { { x }^{ n\quad +\quad 1 } }{ n\quad +\quad 1 }$ where ${ x }^{ n }$ is known as the integrand and the answer is called an integral.

Rules of Integration

1. $\int { { x }^{ n } } dx\quad =\quad \frac { { x }^{ n\quad +\quad 1 } }{ n\quad +\quad 1 } \quad +\quad K$

2. If a constant is multiplied with a function then the function will be integrand and the constant will remain as multiplier.

3. If $f\left( x \right)$ and $g\left( x \right)$ are two different functions, then the sum or the difference can be integrated separately i.e

$\int { \left[ f\left( x \right) \quad \pm \quad g\left( x \right) \right] } dx\quad =\quad \int { f\left( x \right) dx\quad \pm \quad } \int { g\left( x \right) dx\quad }$

Now that we have recalled basic rules of integration we move on to several integration techniques that are useful when performing integration. The following techniques are listed below along with examples to help you in understanding them better.

Integration of trigonometric functions

If you remember differentiation of trigonometric functions, it will be very easy for you to learn integration of trigonometric functions as this is just the reverse of differentiation.

Using the reverse result $\frac { d }{ dx } f\left( x \right) \quad =\quad g\left( x \right) \quad \Rightarrow \quad \int { g\left( x \right)dx\quad =\quad f\left( x \right)\quad +\quad C }$ we obtain the following integrals directly:

i) $\frac { d }{ dx } (sin\quad x)\quad =\quad cos\quad x\quad \rightarrow \quad \int { cos(x) } dx\quad =\quad sin(x)\quad +\quad C$

ii) $\frac { d }{ dx } (cos\quad x)\quad =\quad -sin\quad x\quad \rightarrow \quad \int { sin(x) } dx\quad =\quad -cos(x)\quad +\quad C$

iii) $\frac { d }{ dx } (tan\quad x)\quad =\quad { sec }^{ 2 }\quad x\quad \rightarrow \quad \int { { sec }^{ 2 }(x) } dx\quad =\quad tan(x)\quad +\quad C$

iv)

$\frac { d }{ dx } (sec\quad x)\quad =\quad sec(x)tan(x)\quad \rightarrow \quad \int sec(x)tan(x)dx\quad =\quad sec(x)\quad +\quad C$

$\frac { d }{ dx } (cosec\quad x)\quad =\quad -cosec(x)cot(x)\quad \rightarrow \quad \int cosec(x)cot(x)dx\quad =\quad -cosec(x)\quad +\quad C$

vi) $\frac { d }{ dx } (cot\quad x)\quad =\quad -{ cosec }^{ 2 }\quad x\quad \rightarrow \quad \int { cosec } ^{ 2 }(x)dx\quad =\quad -cot(x)\quad +\quad C$

Example #1

Q. Evaluate $\int _{ 0 }^{ { \pi }/{ 4 } }{ { sec }^{ 2 }(x) } dx$

Solution:

$=\quad \int _{ 0 }^{ { \pi }/{ 4 } }{ { sec }^{ 2 }(x) } dx$

$=\quad { \left[ tan(x) \right] }_{ 0 }^{ { \pi }/{ 4 } }$

$=\quad tan\frac { \pi }{ 4 } \quad -\quad tan(0)$

$=\quad 1\quad -\quad 0$

Ans: $=\quad 1$

Integration of exponential functions

We already know that $\frac { d }{ dx } { (e }^{ x })\quad =\quad { e }^{ x }$ , therefore integration of $e^{ x }$ is:

$\int { e^{ x }dx } \quad =\quad e^{ x }\quad +\quad C$

Also $\frac { d }{ dx } ({ e }^{ \alpha x })\quad =\quad \alpha { e }^{ x }$ therefore:

$\int { { e }^{ \alpha x }\quad dx\quad =\quad \frac { { e }^{ \alpha x } }{ \alpha } } \quad +\quad C$

Example #2

Q. Evaluate $\int { { ({ e }^{ x }\quad +\quad { e }^{ -x }) }^{ 2 } } dx$

Solution:

$=\quad \int { { ({ e }^{ x }\quad +\quad { e }^{ -x }) }^{ 2 } } dx$

$=\quad \int { { { ({ e }^{ x }) }^{ 2 }\quad +\quad ({ e }^{ -x }) }^{ 2 }\quad +\quad 2{ e }^{ x }{ e }^{ -x } } dx$

$=\quad \int { { { ({ e }^{ 2x }) }\quad +\quad ({ e }^{ -2x }) }\quad +\quad 2 } dx$

Ans: $=\quad (\frac { { e }^{ 2x } }{ 2 } \quad -\quad \frac { { e }^{ -2x } }{ 2 } \quad +2x)\quad +\quad C$

Integration of 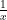$\frac { 1 }{ x }$

We know that $\frac { d }{ dx } ln(x)\quad =\quad \frac { 1 }{ x }$ , therefore:

$\int { \frac { 1 }{ x } \quad dx\quad =\quad ln(x) } \quad +\quad C$

Also if:

$\frac { d }{ dx } ln(ax\quad +\quad b)\quad =\quad \frac { 1 }{ ax\quad +\quad b } \quad \times \quad a$

Hence: $=\quad \frac { a }{ ax\quad +\quad b }$

We have a generalised formula for the above technique:

$\int { \frac { f^{ ' }\left( x \right) }{ f\left( x \right) } } dx\quad =\quad ln\left| f\left( x \right) \right| \quad +\quad C$

Example #3

Q. Evaluate $\int { \frac { 1 }{ 4\quad -\quad 3x } } dx$

Solution:

$=\quad \int { \frac { 1 }{ 4\quad -\quad 3x } } dx$

To be able to use the technique above we must have the derivative of the denominator in the numerator. Thus, to get that form we multiply and divide the above expression by the derivative of the denominator which is “-3” .

$=\quad \frac { 1 }{ -3 } \int { \frac { -3 }{ 4\quad -\quad 3x } } dx$

Now using the technique we get:

Ans: $=\quad \frac { 1 }{ -3 } ln\left| 4\quad -\quad 3x \right| \quad +\quad C$

Integrating Fractions

We have three types here:

1. Type 1: In this type the numerator is a complete derivatives of the denominator. In this case we use the formula: $\int { \frac { f^{ ' }\left( x \right) }{ f\left( x \right) } } dx\quad =\quad ln\left| f\left( x \right) \right| \quad +\quad C$ .

2. Type 2: In this type the numerator is the derivative of a function within the denominator. i.e $\int { \frac { 2x }{ \sqrt { { x }^{ 2 }\quad +\quad 3 } } }$ , where 2x is the derivative of ${ x }^{ 2 }\quad +\quad 3$ .

3. Type 3: If the denominator of the given integrand consists of two or more functions in the form of a product, then partial fractions are very useful in solving such functions.

Example #4

Q. Evaluate $\int { \frac { dx }{ { x }^{ 2 }\quad +\quad 3x\quad +\quad 2 } }$

Solution:

We use partial fractions to solve this:

$\int { \frac { dx }{ { x }^{ 2 }\quad +\quad 3x\quad +\quad 2 } } \quad =\quad \frac { 1 }{ (x\quad +\quad 2)(x\quad +\quad 1) }$

$\int { \frac { 1 }{ (x\quad +\quad 2)(x\quad +\quad 1) } } \quad =\quad \int { \frac { A }{ x\quad +\quad 1 } } \quad +\quad \int { \frac { B }{ x\quad +\quad 2 } }$

$1\quad =\quad A(x\quad +\quad 2)\quad +\quad B(x\quad +\quad 1)$

Putting $x\quad =\quad -2$ ,

$B\quad =\quad -1$

Putting $x\quad =\quad -1$

$A\quad =\quad 1$ , so we get

$\int { \frac { 1 }{ (x\quad +\quad 2)(x\quad +\quad 1) } dx } \quad =\quad \int { \frac { 1 }{ x\quad +\quad 1 } dx } \quad +\quad \int { \frac { -1 }{ x\quad +\quad 2 } } dx$

$=\quad ln\left| x\quad +\quad 1 \right| \quad -\quad ln\left| x\quad +\quad 2 \right| \quad +\quad C$

Partial Fractions are explained in detail in the article ”Partial Fractions”.